De-Broglie's Law
If electromagnetic radiation consists of photons-localized clumps of energy-how can we explain phenomena such as diffraction and interference? If not, then why did Compton have to use classical collision theory to explain the scattering of x rays by metals? On the other hand, if electrons are particles, why do they produce an interference pattern at the detector in the double-slit experiment? The behavior of electrons and photons in these experiments seems provocatively similar---crazy, to be sure, but crazy in the same way. Are electrons and photons in some sense the same?
Einstein was deeply puzzled by this question until he noticed a possible answer in the doctoral thesis of a young French physicist. In 1924, Einstein wrote in a letter to his Dutch colleague Hendrik Lorentz (1853-1928) that the research of Prince Louis de Broglie (1892-1975) .....is the first feeble ray of light to illuminate this, the worst of our physical riddles." De Broglie's achievement was to synthesize the wave-like and particle-like aspects of microscopic matter. Although de Broglie seems to have only dimly understood the nature of quantum particles, and his rather nebulous physical models of quanta have since been superseded, the importance of his contribution has not diminished. It initiated the development of modem quantum mechanics.
In 1910 de Broglie began studying history at the University of Paris; soon, however, he switched to physics. His studies were interrupted in 1913 by a six-year stint in the French army, during which he and his brother Maurice worked on wireless telegraphy. Then in 1919 he returned to Paris for his doctoral research. From work on the x-ray spectra of heavy elements, de Broglie knew of photons and the Bohr model of atomic structure. And he was particularly intrigued by "Planck's mysterious quanta." So he set himself the task of "[uniting] the corpuscular and undulatory points of view and thus [penetrating] a bit into the real nature of quanta." In 1923, lightning struck. As de Broglie tells it:
As in my conversations with my brother we always arrived at the conclusion that in the case of x-rays one had [both] waves and corpuscles, thus suddenly-I cannot give the exact date when it happened, but it was certainly in the course of summer 1923-I got the idea that one had to extend this duality to the material particles, especially to electrons.
Thus did de Broglie come up with the idea of matter waves. This idea led him to the important notion that all microscopic material particles are characterized by a wavelength and a frequency, just like photons. Aesthetic considerations seem to have influenced de Broglie's thinking towards the idea of matter waves. He evidently felt that nature should be symmetrical, so if particles of light (photons) were to be associated with electromagnetic radiation, then so should waves of matter be associated with electrons. Simply stated, his hypothesis is this: There is associated with the motion of every material particle a "fictitious wave" that somehow guides the motion of its quantum of energy.
In spite of its rather vague character, this idea was remarkably successful. For example, using the methods of classical optics (such as Fermat's principle) to describe the propagation of quanta, de Broglie was able to explain how photons (and, for that matter, electrons) diffract and interfere: It is not the particles themselves but rather their "guide waves" that diffract and interfere. In de Broglie's words, "the fundamental bond which unites the two great principles of geometrical optics and of dynamics is thus fully brought to light." De Broglie proffered these ideas in his Ph.D. dissertation, which he wrote at age 31. His thesis did not fully convince his examiners, who were impressed but skeptical of the physical reality of de Broglie's matter waves. One examiner later wrote, "at the time of the defense of the thesis, I did not believe in the physical reality of the waves associated with the particles of matter. Rather, I regarded them as very interesting objects of imagination. Nevertheless, de Broglie passed.
De-Broglie's equation
De Broglie's equations for the wavelength and frequency of his matter waves are elegant and simple. Even their derivations are not complicated. In his seminal paper of 1923,
de Broglie began with light quanta-photons-so I'll first recap the derivation of the equation relating the wavelength and momentum of a photon and then press on to material particles.
The photon is a relativistic particle of rest mass mo = O. Hence the momentum p of a photon is related to its total energy E through the speed of light C as
To introduce the frequency v of the photon, we use Einstein's equation for the photon energy
to write Eq. (2.10) as
For a wave in free space, the wavelength is 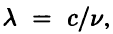 , so Eq. (2.12) becomes
, so Eq. (2.12) becomes
The source:
Michael A. Morrison - Understanding Quantum Physics.
By. Fady Tarek









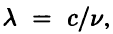 , so Eq. (2.12) becomes
, so Eq. (2.12) becomes

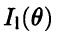


 of Eq. (2.6) provided we assign to each electron (of mass m and energy E) a wavelength
of Eq. (2.6) provided we assign to each electron (of mass m and energy E) a wavelength









