Parabola of the third degree
Simple case
This equation has a graph in the form of a curve called a
parabola of the third degree. We shall consider the simplest case of this
curve:
For a positive, the signs of x and y are the same; for a negative,
they are different. In the first case, the curve lies in the first and third
quadrants of the coordinate axes, and in the second case, it lies in the second
and fourth quadrants. Figure 17 illustrates the form of the curve for various
values of a.

If x and y change simultaneously to (-x) and (-y), both
sides of equation (8) change sign, and the equation is not essentially altered,
i.e. if the point (x, y) lies on the curve (8), the point (-x, -y) also lies on
this curve. The points (x, y) and (-x, -y) are evidently symmetrical relative
to the origin O, i.e. the line joining them is bisected at O. It follows from
this that every chord of the curve (8) that passes through the origin of
coordinates O is bisected there. In other words: the origin of coordinates O is
the center of the curve (8).
Another case
A further particular case of a third-degree parabola will be
mentioned:
The right-hand side of this equation is the sum of two
terms, and consequently, to construct the curve, it is sufficient to draw the
straight line:

and take the sums of corresponding ordinates (y value) of
graphs (8) and (10) directly from the figure. Figure 18 illustrates the various
forms that the curve (9) assumes (with a = 1, and various c).

If the curve

is drawn, we obtain a convenient, though not too accurate,
method for solving graphically an equation of the third degree:

the roots of this equation being, in fact, the abscissa of
the points of intersection of the curve y = x^3 with the line

As can be seen from the figure (Fig.19), there may be one,
two, or three points of intersection, but there must be at least one, i.e. an
equation of the third degree must have at least one real root.

the source:
A COURSE OF Higher Mathematics VOLUME I. SMIRNOV.
By: Fady tarek






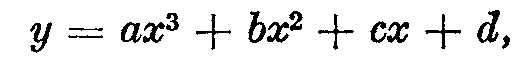










0 comments:
Post a Comment