Bohr's Principle of Complementarity

Bohr's Principle of Complementarity

Bohr was 'one of the intellectual giants of early quantum theory. His ideas and his personality were enormously influential. During the twenties and thirties, the Bohr Institute in Copenhagen (which was financially supported by the Carlsberg Brewery) became a haven for scientists who were developing the new physics. Bohr was not always receptive to quantum ideas; like many of his colleagues, he initially rejected Einstein's photons. But by 1925 the overwhelming experimental evidence that light actually has a dual nature had convinced him. So for the next several years, Bohr concentrated on the logical problem implied by this duality, which he considered the central mystery of the interpretation of quantum theory. Unlike many of his colleagues, Bohr emphasized the mathematical formalism of quantum mechanics. Like de Broglie, he considered it vital to reconcile the apparently contradictory aspects of quanta. Bohr's uneasy marriage of the wave and particle models was the Principle of Complementary. This principle entails two related ideas:

1-A complete description of the observed behavior of microscopic particles requires concepts and properties that are mutually exclusive .

2-The mutually exclusive aspects of quanta do not reveal themselves in the same observations.

The second point was Bohr's answer to the apparent paradox of wave-particle duality: There is no paradox. In a given observation, either quanta behave like waves or like particles.

How, you may wonder, could Bohr get away with this-eliminating a paradox by claiming that it does not exist because it cannot be observed? Well, he has slipped through a logical loophole provided by the limitation of quantum physics that quantum mechanics describes only observed phenomena. From this vantage point, the central question of wave-particle duality is not "can a thing be both a wave and a particle?" Rather, the question is "can a thing be observed behaving like a wave and a particle in the same measurement?" Bohr's answer is no: in a given observation, quantum particles exhibit either wave-like behavior (if we observe their propagation) or particle-like behavior (if we observe their interaction with matter). And, sure enough , no one has yet found an exception to this principle.

Notice that by restricting ourselves to observed phenomena, we are dodging the question, "what is the nature of the reality behind the phenomena?" Many quantum physicists answer, "there is no reality behind phenomena." But that is another story.

The source:

Michael A. Morrison - Understanding Quantum Physics.

By. Fady Tarek

Read More

De-Broglie's Law

De-Broglie's Law

If electromagnetic radiation consists of photons-localized clumps of energy-how can we explain phenomena such as diffraction and interference? If not, then why did Compton have to use classical collision theory to explain the scattering of x rays by metals? On the other hand, if electrons are particles, why do they produce an interference pattern at the detector in the double-slit experiment? The behavior of electrons and photons in these experiments seems provocatively similar---crazy, to be sure, but crazy in the same way. Are electrons and photons in some sense the same?

Einstein was deeply puzzled by this question until he noticed a possible answer in the doctoral thesis of a young French physicist. In 1924, Einstein wrote in a letter to his Dutch colleague Hendrik Lorentz (1853-1928) that the research of Prince Louis de Broglie (1892-1975) .....is the first feeble ray of light to illuminate this, the worst of our physical riddles." De Broglie's achievement was to synthesize the wave-like and particle-like aspects of microscopic matter. Although de Broglie seems to have only dimly understood the nature of quantum particles, and his rather nebulous physical models of quanta have since been superseded, the importance of his contribution has not diminished. It initiated the development of modem quantum mechanics.

In 1910 de Broglie began studying history at the University of Paris; soon, however, he switched to physics. His studies were interrupted in 1913 by a six-year stint in the French army, during which he and his brother Maurice worked on wireless telegraphy. Then in 1919 he returned to Paris for his doctoral research. From work on the x-ray spectra of heavy elements, de Broglie knew of photons and the Bohr model of atomic structure. And he was particularly intrigued by "Planck's mysterious quanta." So he set himself the task of "[uniting] the corpuscular and undulatory points of view and thus [penetrating] a bit into the real nature of quanta." In 1923, lightning struck. As de Broglie tells it:

As in my conversations with my brother we always arrived at the conclusion that in the case of x-rays one had [both] waves and corpuscles, thus suddenly-I cannot give the exact date when it happened, but it was certainly in the course of summer 1923-I got the idea that one had to extend this duality to the material particles, especially to electrons.

Thus did de Broglie come up with the idea of matter waves. This idea led him to the important notion that all microscopic material particles are characterized by a wavelength and a frequency, just like photons. Aesthetic considerations seem to have influenced de Broglie's thinking towards the idea of matter waves. He evidently felt that nature should be symmetrical, so if particles of light (photons) were to be associated with electromagnetic radiation, then so should waves of matter be associated with electrons. Simply stated, his hypothesis is this: There is associated with the motion of every material particle a "fictitious wave" that somehow guides the motion of its quantum of energy.

In spite of its rather vague character, this idea was remarkably successful. For example, using the methods of classical optics (such as Fermat's principle) to describe the propagation of quanta, de Broglie was able to explain how photons (and, for that matter, electrons) diffract and interfere: It is not the particles themselves but rather their "guide waves" that diffract and interfere. In de Broglie's words, "the fundamental bond which unites the two great principles of geometrical optics and of dynamics is thus fully brought to light." De Broglie proffered these ideas in his Ph.D. dissertation, which he wrote at age 31. His thesis did not fully convince his examiners, who were impressed but skeptical of the physical reality of de Broglie's matter waves. One examiner later wrote, "at the time of the defense of the thesis, I did not believe in the physical reality of the waves associated with the particles of matter. Rather, I regarded them as very interesting objects of imagination. Nevertheless, de Broglie passed.

De-Broglie's equation

De Broglie's equations for the wavelength and frequency of his matter waves are elegant and simple. Even their derivations are not complicated. In his seminal paper of 1923,

de Broglie began with light quanta-photons-so I'll first recap the derivation of the equation relating the wavelength and momentum of a photon and then press on to material particles.

The photon is a relativistic particle of rest mass mo = O. Hence the momentum p of a photon is related to its total energy E through the speed of light C as

To introduce the frequency v of the photon, we use Einstein's equation for the photon energy

to write Eq. (2.10) as

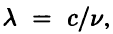For a wave in free space, the wavelength is , so Eq. (2.12) becomes

The source:

Michael A. Morrison - Understanding Quantum Physics.

By. Fady Tarek

Read More

interference experiment of electrons

interference experiment of electrons

Our strategy in the double-slit experiment is to send electrons through a double-slit diaphragm and see how the intensity measured by the detector differs from the interference pattern formed by light. To implement this strategy, we must make a few modifications in the apparatus Young used when he performed this experiment with light. First we replace the light source with an electron gun-a device that produces a (nearly monoenergetic) beam of electrons of energy E. A heated tungsten wire, for example, produces a stream of electrons that we can accelerate to the desired velocity. Second, we replace the photographic plate with an electron detector: a device that counts the number of electrons that arrive in each square meter of unit area per sec. (Like the photographic plate used in Young's experiment, our electron detector measures the rate at which energy arrives at each point on the detector.) A screen covered with phosphor will do; when an electron arrives at the screen, it produces a spot.

What would we expect to see at the detector if the electrons were particles, subject to the same physical laws as, say, marbles? Imagine for a moment that we block one slit-say, the lower slit in Fig. 2.3-so that all electrons must come through the other, open slit. Most electrons that make it through the diaphragm will go straight through this slit, "piling up" at the detector directly opposite it. We therefore expect to see a maximum in the measured intensity opposite the upper slit. But some particles will scatter from the edges of this slit, so we expect some amount of spread in the pattern. A reasonable guess for the intensity for a beam of particles passing through this apparatus with only the upper slit open is the curve  sketched in Fig. 2.6a. The curve  should be obtained if only the lower slit is open.

What should happen when both slits are open? Well, if the electrons are indeed particles, then the measured intensity should be simply . This rather featureless curve is sketched in Fig. 2.6b. (Were you to scale the apparatus to macroscopic size and send through it a uniform beam of marbles-with, of course, a suitable detector this is what you would see.) But what we actually see when we run the experiment with electrons is altogether different.

The measured intensities in Fig. 2.7 clearly exhibit bands of alternating high and low intensity: an interference pattern, like the one formed by light (see Fig. 2.4). This observation seems to imply that the electrons are diffracted by the slits at the diaphragm and then interfere in the region between the diaphragm and the detector. 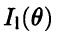We can even fit the measured intensity of the scattered electrons to the double-slit function  of Eq. (2.6) provided we assign to each electron (of mass m and energy E) a wavelength

But to a classical physicist, steeped in the idea that electrons are particles, Eq. (2.9) is nonsense!

The source:

Michael A. Morrison - Understanding Quantum Physics.

By. Fady Tarek

Read More

Understanding interference in classical physics

Understanding interference in classical physics 

The theory of diffraction is the foundation for study of the double-slit interference experiment. When first performed in 1800 by Thomas Young (1773-1829), this experiment was considered definitive proof of the wave nature of light. We can modify the single-slit apparatus of Fig. 2.1 to suit Young's experiment by simply cutting a second slit in the diaphragm.

As shown in Fig. 2.3, the width of the second slit is the same as that of the first, w. We must position the second slit so that the two slits are close together-but not too close: for observable interference to occur, the slit separation s must be greater than w. Again, we shine a beam of monochromatic light of frequency v on the diaphragm and see what happens at the detector, which is far to the right of the diaphragm. Figure 2.3

This time, our detector shows an interference pattern like the one in Fig. 2.4. At first glance, this figure may look similar to the diffraction pattern of Fig. 2.2, but on closer examination we see striking differences. For one thing, the interference pattern exhibits more bright bands than the diffraction pattern. This means that the energy of the radiation scattered by the double-slit diaphragm is more evenly distributed than that scattered by a single slit. (In the diffraction pattern about 90% of the energy appears in the central band.) Finally, the individual bands in the interference pattern, which are called interference fringes, are narrower than those of the diffraction pattern.

If we study how the interference pattern changes as we fiddle with the incident wavelength ., the slit separation s, and the slit width w, we discover that the separation between the bright bands increases with increasing just as it did in the diffraction pattern, for which the separation is proportional to  /w. But also we find a difference: the separation in Fig. 2.4 is independent of the slit width w but is inversely proportional to the slit separation s.

The key to understanding interference is superposition. When the incident plane wave encounters the double-slit diaphragm it "splits," and a diffracted wave emerges from each slit. (In a sense, each slit becomes a source of radiation that travels to the detector.) These waves add in the region between the slit and the detector, and this device measures the intensity of their superposition . Now, at the detector the amplitudes of the electric fields of the diffracted waves are equal, but their phases are not. Consequently, their superposition manifests regions of constructive and destructive interference, as seen in Fig. 2.4.

The trick to deriving an equation for the intensity measured in the double-slit experiment-which we'll call is therefore to add the electric fields of the waves diffracted by each slit. (This step is legitimate because Maxwell's equation for these fields is linear.) Having done so, we could calculate the aforementioned phase difference and would find the field from the lower slit lags the field from the upper slit by an amount . The last step is to average the squared modulus of the total electric field at a point  on the detector over one period, which yields 

The source:

Michael A. Morrison - Understanding Quantum Physics.

By. Fady Tarek

Read More

Understanding diffraction in classical physics

Understanding diffraction in classical physics

Diffraction, which was first observed by Leonardo da Vinci, is often considered to be the signature of a wave. Diffraction occurs when ripples in a pond encounter a pair of logs that are close together, when light passes through a narrow slit in a window shade, or when x-rays scatter from a crystal. In each case, we can explain the distinctive pattern that forms using classical wave theory. Understand what happens to a wave when it passes through a small aperture-that is, understand diffraction-and you are well on your way to understanding the behavior of waves in more complicated situation.

A schematic of a single-slit diffraction experiment with light is shown in Fig. 2.1. Monochromatic light of frequency v is incident on a diaphragm in which there is a single slit of width w.

 We'll assume that the light source is far to the left of the diaphragm, so the incident radiation can be represented by a plane wave. The width of the slit must be small compared to the wavelength  = c/v of the radiation if the slit is to appreciably diffract the light; for example, to diffract visible light enough to observe this phenomenon, we require a slit of width w=10^-4 cm. Light scattered by the diaphragm falls on a detector, such as a photographic plate or a photocell, located at a distance D far to the right of the slit. The detector measures the energy delivered by the scattered wave as a function of the distance x in Fig. 2.1.

Light scattered by the single-slit diaphragm forms a beautiful diffraction pattern at the detector. This pattern is characterized by a very bright central band located directly opposite to the slit, surrounded by a series of alternating light and dark regions. The light regions on either side of the central band are called secondary hands, because they are much less intense than the central band. Indeed, the intensity of the secondary bands drops off so dramatically on either side of the central band that only one pair of secondary bands is visible. Additional weak secondary bands exist, though, as you can see in Fig. 2.2, which is a graph of the intensity measured by the detector. If we play around with the frequency control on the light source and study the resulting diffraction patterns, we discover that the separation between adjacent bright bands is proportional to the wavelength of the incident radiation.

A classical physicist would call upon Maxwell's electromagnetic wave theory to explain the pattern in Fig. 2.2. To understand qualitatively what happens when a plane wave passes through a diaphragm we invoke Huygens's Principle, which lets us replace the plane wave and the slit (in our mind's eye) by a large number of closely-spaced , discrete radiating charges that fill the region of space where the slit is located."Scattered waves" radiated by different oscillators-i.e., waves that emerge from different locations in the slit region-have different phases, so the superposition of these scattered waves exhibits regions of high and low intensity, as in Fig. 2.2.

to derive an expression for the electric field at a point (r, ) on the detector (see Fig. 2.1). But the quantity measured in this experiment is not the electric field; it is the intensity the rate at which the scattered radiation delivers energy to the detector. This quantity is proportional to the time-averaged energy flux-i.e., to the average over one period of the square of the modulus of the electric field. I'll denote by  the intensity at a fixed value of r due to radiation scattered by a single slit.

Omitting the details of the derivation of , I'll just quote the result. For convenience, I'll write the intensity in terms of its value  at the principal maximum i.e, at the point r=D, ( = 0, in the central peak in Fig. 2.2-and the handy intermediate quantity

the single-slit intensity at fixed r is

The intensity (2.4) is graphed in Fig. 2.2 as a function of w sin(); plotted this way, exhibits a characteristic pattern of equally-spaced nodes [where  = 0], which occur at

The principal (zeroth-order) maximum of the intensity pattern and higher order maximum occur (approximately) at

Equation (2.4) fully accounts for the properties of patterns such as the one in Fig. 2.2. Thus does classical electromagnetic theory rend the veil of mystery from the phenomenon of diffraction.

The source:

Michael A. Morrison - Understanding Quantum Physics.

By. Fady Tarek

Read More

Basic theorems of limits

Basic theorems of limits

1-The limit of the algebraic sum of a finite number of variables is equal to the sum of their limits.

For the sake of exactness let us take the algebraic sum x-y+z of three simultaneously varying magnitudes. We suppose that x, y and z tend respectively to limits a, b and c. We show that the sum tends to the limit a - b + c.

We have:

where  are infinitesimals. We can write for the sum:

The first bracket on the right-hand side of this equation is a constant, and the second is an infinitesimal. Hence:

2-The limit of the product of a finite number of variables is equal to the product of their limits.

We confine ourselves to the case of the product x*y of two variables. We suppose that x and y vary simultaneously, tending respectively to limits a and b, and we show that x*y tends to the limit a*b.

We have by hypothesis:

where  are infinitesimals; hence:

Using both of the properties of infinitesimals, we see that the sum in the bracket on the right of this equation is an infinitesimal, and hence we have:

3-The limit of a quotient is equal to the quotient of the limits, provided the limit of the denominator is not zero.

We take the quotient x/y, and suppose that x and y tend simultaneously to their respective limits a and b, where  We show that x/y tends to a/b.

To prove the theorem, it is sufficient to show that the difference a/b - x/y is an infinitesimal. By hypothesis:

where  are infinitesimals. Hence:

The denominator of the fraction on the right of this equation is the product of two factors, and tends to b^2. Thus, from some initial moment of its variation, it is greater than b^2/2, the fraction as a whole being included between zero and 2/b^2, i.e. the fraction is bounded. The term  is an infinitesimal. Hence, the difference a/b-x/y is an infinitesimal, and

the source:

A COURSE OF Higher Mathematics VOLUME I. SMIRNOV.

By: Fady tarek

Read More